拉普拉斯近似与贝叶斯逻辑回归——PRML第四章(3)

在之前讲到的方法中，我们假设模型后，会通过最大似然估计或者最大后验概率估计推断出模型的最优参数，然后在该参数条件下使用判别概率分布做决断，即通过$p(C_k|\mathbf{x}, \mathbf{w}^{ML} / \mathbf{w}^{MAP})$做决断。这种方法实际上是从参数$\mathbf{w}$的分布上取一个最有可能的出现的参数（概率密度最大）作为模型的最终参数，而忽略了其他参数出现的可能性，不可避免产生过拟合问题，贝叶斯方法就是为了解决这一问题。

贝叶斯方法

在之前的方法中，决策阶段只考虑可能性最大的参数，即$\mathbf{w}^{ML}$或$\mathbf{w}^{MAP}$，贝叶斯方法则考虑所有可能的参数。之前的方法通过判别概率来进行决策$p(C_k|\mathbf{x},\mathbf{w})$，贝叶斯方法通过预测分布（Predictive distribution）来决策，即

$$p(C_k|\mathbf{x},\mathbf{t}) = \int p(C_k|\mathbf{x},\mathbf{w})p(\mathbf{w|t})d \mathbf{w} \tag{1}$$

其中$\mathbf{t}$指整个数据集。

上式可以看成一个加权平均，对于每种可能的参数$\mathbf{w}$，其判别的结果$p(C_k|\mathbf{x},\mathbf{w})$需乘上参数$\mathbf{w}$出现的概率。这很像一种集成学习，可以有效提高模型的泛化能力。

拉普拉斯近似

在介绍贝叶斯逻辑回归之前，先讲一个预备知识——拉普拉斯近似。

很多时候我们需要求一个概率分布的积分，但是这个概率分布的积分很难求甚至不可求怎么办？一个直接的方法是用一个比较好求的相似的概率分布去代替这个概率分布。拉普拉斯近似就是用一种用高斯分布去近似其他分布的方法。

假设需要近似的概率分布为：

$$p(z) = \frac{1}{Z}f(z)$$

其中$Z$是归一化系数。

在用高斯分布去近似原始分布时，高斯分布均值的位置应该在原始分布概率密度取最大值的位置，即$z_0$：

$$\left.\frac{df(z)}{dz} \right|_{z=z_0} = 0$$

同时，由于对高斯分布取$\ln$可以得到二次项，可以对原始分布取$\ln$再做Taylor展开：

$$\ln f(z) \simeq \ln f(z_0)-\frac{1}{2}A(z-z_0)^2$$

其中一次项由于$z_0$是驻点等于0，

$$A = \left. -\frac{d^2}{dz^2}\ln f(z) \right|_{z=z_0}$$

由此可得到：

$$f(z) \simeq f(z_0)\exp{\left\{ -\frac{A}{2}(z-z_0)^2 \right\}}$$

即高斯分布的均值为$z_0$，准确率为$A$，则近似的高斯分布为：

$$q(z) = \left( \frac{A}{2\pi} \right) ^ {1/2} \exp{\left\{ -\frac{A}{2}(z-z_0)^2 \right\}} \tag{2}$$

值得注意的是，应该要求$f(z)​$在$z_0​$处取得最大值，$A​$需要大于0。

对于高维情况，使用同样的处理方法得到近似的高斯分布如下：

$$q(\mathbf{z}) = \frac{|\mathbf{A}|^{1/2}}{(2\pi)^{M/2}}\exp{ \left\{ -\frac{1}{2} \mathbf{(z-z_0)^{T}A(z-z_0)}\right\} } \tag{3}$$

$\mathbf{A}$需要是正定的。

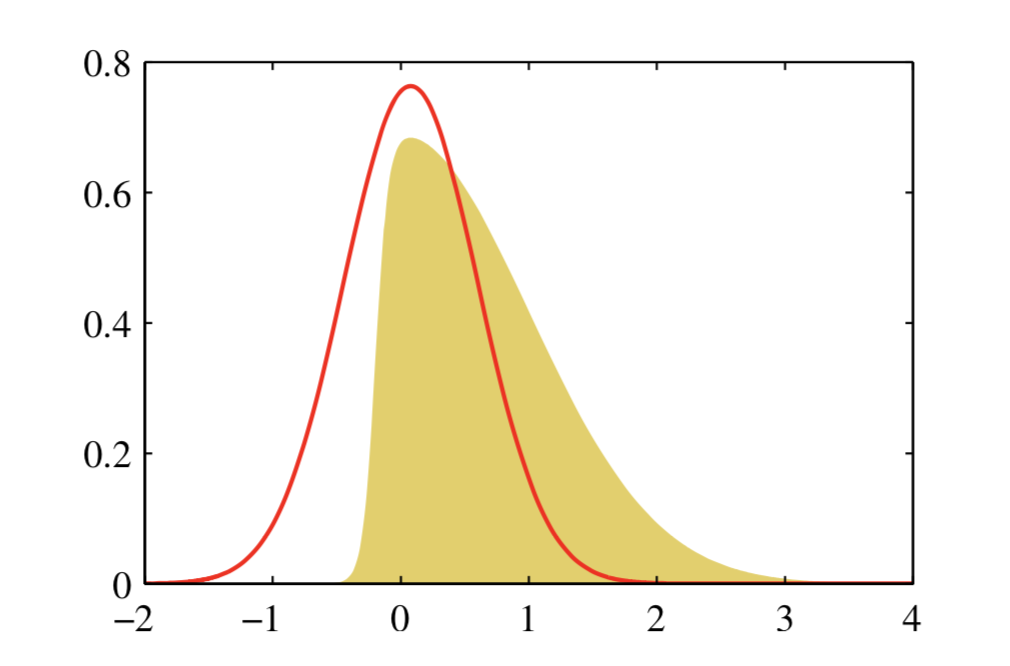
拉普拉斯的近似效果如下：

贝叶斯逻辑回归

对于二分类逻辑回归模型，其预测分布为：

$$p(C_1|\mathbf{x},\mathbf{t}) = \int p(C_1|\mathbf{x}, \mathbf{w})p(\mathbf{w}|\mathbf{t})d\mathbf{w} = \int \sigma(\mathbf{w^Tx})p(\mathbf{w}|\mathbf{t})d\mathbf{w} \tag{4}$$

因为后验概率$p(\mathbf{w|t})$不好求，我们可以用高斯分布去近似。

$$p(\mathbf{w|t}) \propto p(\mathbf{w})p(\mathbf{t|w})$$

假设先验概率$p(\mathbf{w}) = N(\mathbf{w|m_0,S_0})$，则

$$\ln{p(\mathbf{w|t})} = -\frac{1}{2}\mathbf{(w-w_0)^TS_0^{-1}(w-w_0)} + \sum_{1}^{N} \left\{ t_n \ln y_n + (1-t_n) \ln (1 -y_n) \right\}+ const$$

其中$yn = \sigma(\mathbf{w^Tx})$，上式求一次导等于0的解正好是最大后验概率估计的解$\mathbf{w}_{MAP}$，对上式求二次导得到

$$\mathbf{S}_N=-\mathbf{\bigtriangledown\bigtriangledown} \ln p(\mathbf{w|t}) = \mathbf{S_0}^{-1}+ \sum_{n=1}^{N}y_n(1-y_n)\mathbf{xx^T}$$

因此近似的高斯分布为：

$$q(\mathbf{w})=N(\mathbf{w}|\mathbf{w}_{MAP},\mathbf{S}_N^{-1})$$

则式（4）近似等于

$$p(C_1|\mathbf{x},\mathbf{t}) = \int \sigma(\mathbf{w^Tx})p(\mathbf{w}|\mathbf{t})d\mathbf{w} =\int \sigma(\mathbf{w^Tx})q(\mathbf{w})d\mathbf{w} \tag{5}$$

为了方便计算，引入Dirac delta function，也叫奇点分布。这是一个极端的概率分布，其所有的概率密度都集中在一个点上，其分布图如下：

奇点分布可看成一种极端的高斯分布，其有如下性质：

$$\int f(x)\delta(x)dx=f(0)$$

根据以上性质有(使用换元$u = a-\mathbf{w^Tx}$)：

$$\sigma(\mathbf{w^Tx}) = \int \delta(a-\mathbf{w^Tx})\sigma(a)da$$

则

$$\begin{aligned} \int \sigma(\mathbf{w^Tx})q(\mathbf{w})d\mathbf{w} & = \int \int \delta(a-\mathbf{w^Tx})\sigma(a)\text{d}a q(\mathbf{w}) \text{d}\mathbf{w} \\ &= \int \sigma(a)\int \delta(a-\mathbf{w^Tx}) q(\mathbf{w}) \text{d}\mathbf{w}\text{d}a \\ &= \int \sigma(a)p(a)\text{d}a \end{aligned}$$

其中$p(a) = \int \delta(a-\mathbf{w^Tx}) q(\mathbf{w}) \text{d}\mathbf{w}​$。

可以推断出$p(a)$是高斯分布，有两种解释：

1. 因Dirac delta function可也看成一个高斯分布，$q(\mathbf{w})$也是高斯分布，高斯分布的边缘概率是高斯分布
2. 因Dirac delta function只在0处有值，其他地方均为0，$\delta(a-\mathbf{w^Tx})$可以看成对$\mathbf{w}$做了线性约束，$p(a)$可看成从联合概率密度$q(\mathbf{w})$中积掉了一部分，也是求边缘概率，所以也是高斯分布。（这一点是书上的解释，尚未理解透彻）

既然知道$p(a)$是高斯分布，只要把均值方差求出来分布就出来了：

$$\begin{aligned} \mu_a = E(a) = \int p(a)a \text{d}a &= \int \int \delta(a-\mathbf{w^Tx}) q(\mathbf{w}) \text{d}\mathbf{w} a \text{d}a \\ & = \int \int \delta(a-\mathbf{w^Tx})a \text{d}a~ q(\mathbf{w}) \text{d}\mathbf{w} \\ & = \int \mathbf{w^Tx}~ q(\mathbf{w}) \text{d}\mathbf{w} = \mathbf{w_{MAP}^Tx} \end{aligned}$$ $$\sigma_a^2 = \text{var}(a) =\int p(a)\lbrace a^2-E(a)^2 \rbrace = \int q(\mathbf{w}) \lbrace (\mathbf{w^Tx})^2-\mathbf{w_{MAP}^Tx})^2\rbrace = \mathbf{x^TS_Nx}$$

所以式（5）等于：

$$p(C_1|\mathbf{t}) = \int \sigma(a)p(a)\text{d}a = \int \sigma(a)N(a|\mu_a,\sigma_a^2) \text{d}a \tag{6}$$

虽然已经做了很多，但是式(6)依然不太好求，需要做进一步近似。之前讲过，Inverse probit function的形状跟sigmoid的形状十分相似，正好是高斯分布，用在式(6)中正合适。最终：

$$p(C_1|\mathbf{t}) = \int \sigma(a)N(a|\mu_a,\sigma_a^2) \text{d}a \simeq \int \Phi(\lambda a) N(a|\mu_a,\sigma_a^2) \text{d}a = \Phi(\frac{\mu_a}{(\lambda^{-2}+\sigma_a^2)^{1/2}}) = \sigma\left( k(\sigma_a^2)\mu_a \right)$$

其中$k(\sigma_a^2) = (1+\lambda^2\sigma_a^2)$，$\lambda^2$取$\pi/8$。

贝叶斯模型评价

讲了这么多模型，那什么样的模型比较好呢？在贝叶斯方法中，采用Model Evidence来评价模型好坏：

$$p(D|M_i) = \int p(D|\theta,M_i)p(\theta |M_i) \text{d}\theta$$

其中$M_i$表示假设的模型，如逻辑回归、假设$p(\mathbf{x}|C_k)$为高斯分布的生成模型等，$p(\theta|M_i)$表示在模型假设$M_i$下模型中参数$\theta$的先验，$p(D|\theta,M_i)$表示在参数$\theta$的情况下模型拟合数据集的能力。Model Evidence实际上评估的是模型在参数任取的情况下的平均性能。由于模型假设$M_i$相同，为保持公式的简介，后面公式中都省略$M_i$:

$$p(D) = \int p(D|\theta)p(\theta ) \text{d}\theta \tag{7}$$

因为不知道$p(D|\theta)p(\theta)$的形式，可以用拉普拉斯近似。

对于概率分布$f(\mathbf{z})$，其积分为：

$$Z = \int f(\mathbf{z}) \text{d} \mathbf{z} \simeq f(\mathbf{z}_0) \int \exp \left\{-\frac{1}{2} \mathbf{(z-z_0)^TA(z-z_0)}\right\} = f(\mathbf{z_0}) \frac{(2\pi)^{M/2}}{|\mathbf{A}|^{1/2}}$$

将$p(D)$看做$Z$，$p(D|\theta)p(\theta)$看做$f(\mathbf{z})$，有：

$$p(D) = p(D|\theta_{MAP})p(\theta_{MAP}) + \frac{(2\pi)^{M/2}}{|\mathbf{A}|^{1/2}}$$

对两边取$\ln$之后有：

$$\ln p(D) = \ln p(D|\theta_{MAP}) + \ln p(\theta_{MAP}) + \frac{M}{2}\ln(2\pi)-\frac{1}{2}\ln|\mathbf{A}| \tag{8}$$

第一项表示该模型对数据的拟合程度，后三项是对该模型的惩罚。

如果先验分布比较宽，也就是不做过多假设，并且$\mathbf{A}$是满秩的，则式(8)可以下式近似：

$$\ln p(D) \simeq \ln p(D|\theta_{MAP})-\frac{1}{2}M \ln N \tag{9}$$

上式也称之为BIC准则(Bayesian Information Criterion)，其中$M$表示模型参数个数，$N$表示数据量。从BIC可以看出，一个好的模型不仅应该对数据拟合非常好，而且参数也应尽量少。