使用判别公式进行线性分类——PRML第四章(1)

最近因为要给学弟们讲课，重读了PRML第四章，把之前没读懂的都弄懂了，收获很大，现做个总结。

分类问题的方法可归结三类：判别公式（Discriminant function），生成模型（Generative model）和判别模型（Discriminative model）。后两者都是在概率框架下对概率分布进行建模，区别在于建模对象的不同，之后再详细讲。使用判别公式就相对比较简单粗暴，就是学习一个映射函数，直接将样本映射到标签。

分界面

二分类

对于二分类问题，判别公式的一般形式为：

$$y(x)=\mathbf{w^{T}x}+ w_0 \tag{1}$$

两类之间的分界面为：

$$y(x)=\mathbf{w^{T}x}+ w_0 = 0 \tag{2}$$

下图展示了二维平面上的分界面效果及一些性质。

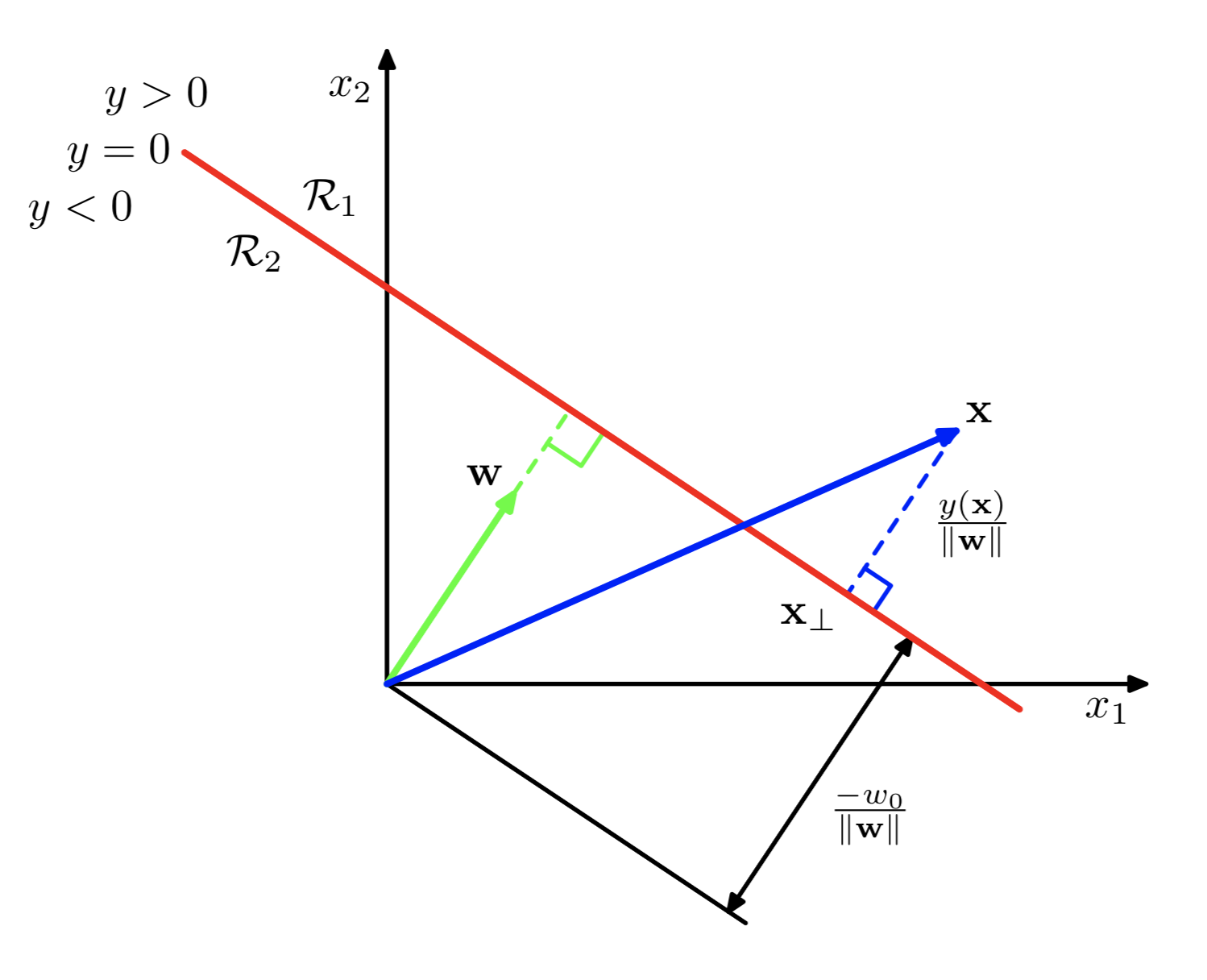
对于平面中的任意一点$\mathbf{x}$，有

$$\mathbf{x} = \mathbf{x_{\perp} } + r \frac{\mathbf{w}}{||\mathbf{w}||}$$

利用(2)，可得打每个点$\mathbf{x}$到分界面的距离:

$$\begin{aligned} &\mathbf{w^{T}x} =\mathbf{w^{T}x_{\perp}} + r \mathbf{\frac{w^Tw}{||w||}} =\mathbf{w^{T}x_{\perp}} + r \mathbf{||w||} \\ &y(\mathbf{x}) = \mathbf{w^{T}x} + w_0 =\mathbf{w^{T}x_{\perp}} + w_0 + r \mathbf{||w||} = r \mathbf{||w||} \\ &r = \frac{y(\mathbf{x})}{\mathbf{||w||}} \end{aligned}$$

多分类

对于多分类问题，构建分界面有几种不同方案

1. One vs Rest：每类和剩下的所有类作分类，构建$K-1$个分类器
2. One vs One：每两类之间构建一个分类器，共$K(K-1)/2$
3. 构建K个分类器，类似于softmax，每个分类器输出一个得分，将样本预测为得分最高的那一类

前两种方法都存在一定缺陷：

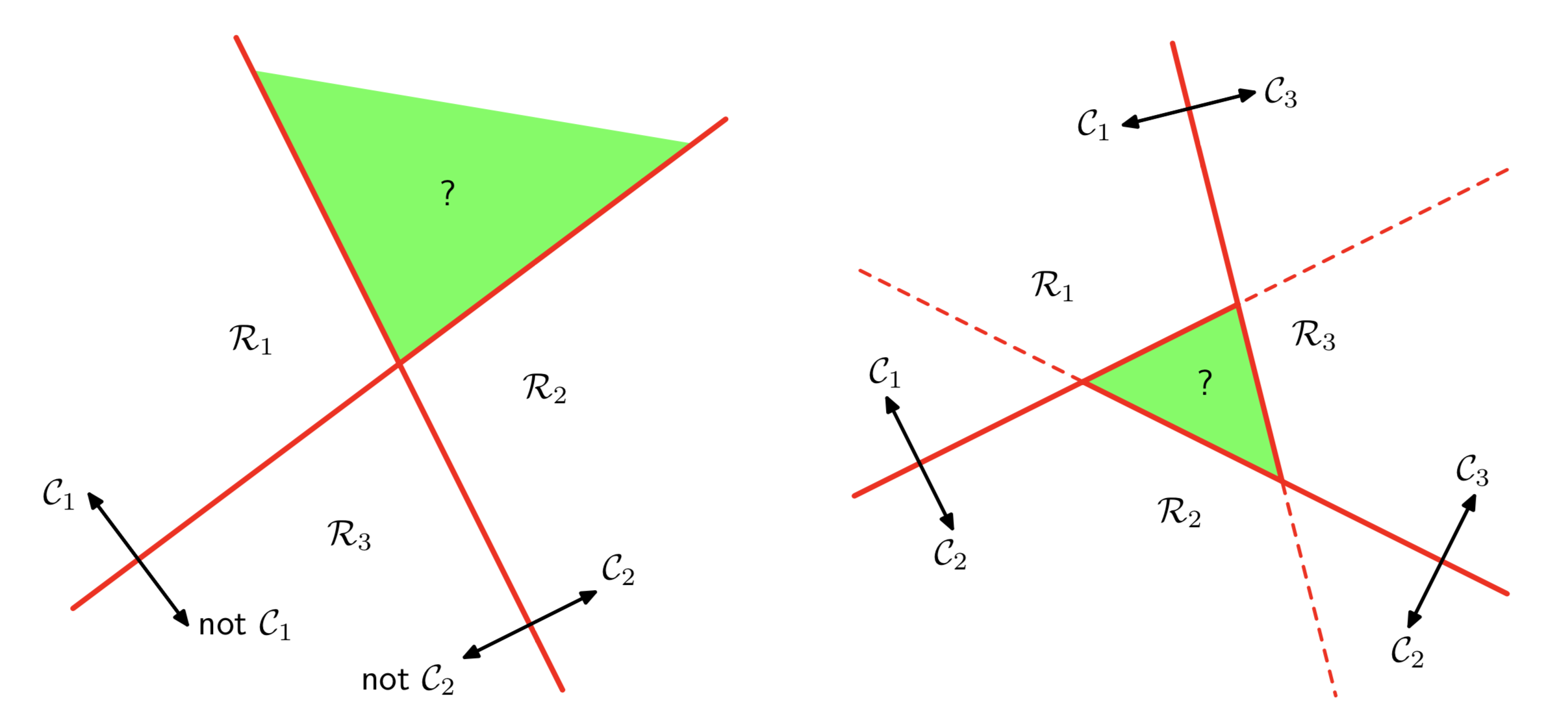
上图左是One vs Rest方法，当两个分类器的分类结果是Yes C1，Yes C2时，无法区分是哪一类，即图中的绿色区域。上图右表示One vs One方法，采用投票的方法确定最后的结果，但是当预测结果轮换时（即classifier(C1, C2) -> C2, classifier(C2, C3) -> C3, classifier(C1, C3) -> C1），无法确定样本属于哪一类。

因以上原因，实际多分类问题中一般采用第3中方式进行多分类。对于K分类问题，其判别公式一般形式为：

$$y_k(\mathbf{x}) = \mathbf{w_{k}^{T}x} + w_{k0} ~~~~~~~k=1, 2,3, \cdots, K \tag{3}$$

任意两类$k,j$之间的分界面为：

$${(\mathbf{w}_{k} - \mathbf{w}_{j})}^{\mathbf{T}}\mathbf{x} + (w_{k0} - w_{j0}) = 0$$

下图展示了分界面效果：

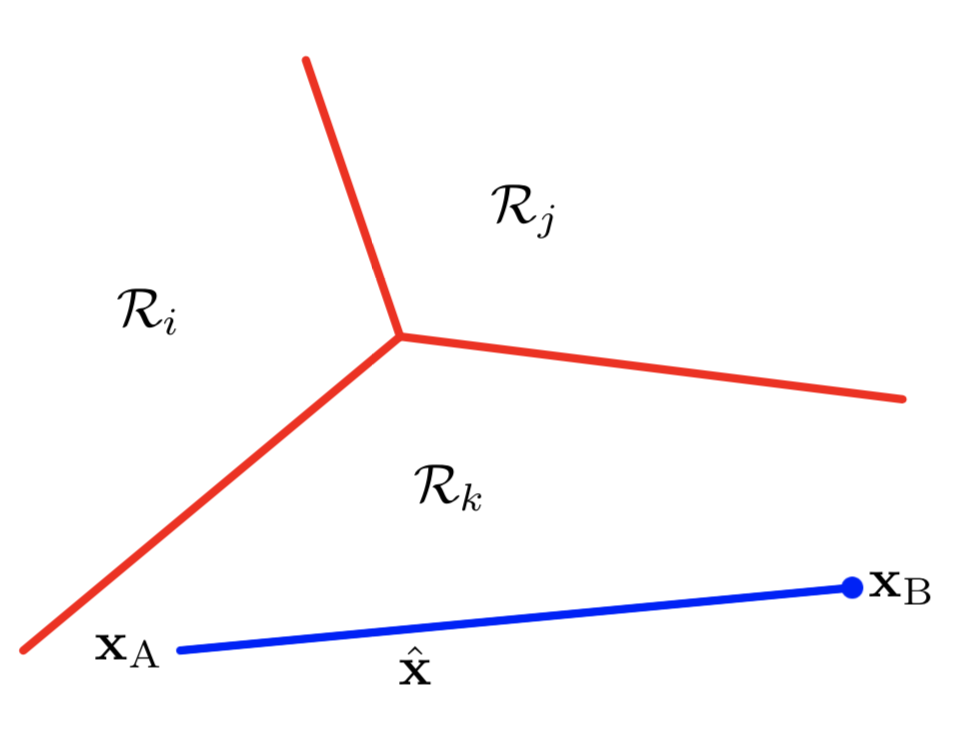
几种分类方法

为后文公式书写方便，对于(1)(3)中判别公式采用以下方式简写：

$$y(x)=\mathbf{w^{T}x} \\ \mathbf{y(x)} = \mathbf{W^{T}x}$$

这种方法将偏置当做$\mathbf{w}$中的一维，其对应维中的$\mathbf{x}$取值为1。

Least squares

一种很容易想到的方法就是用最小二乘法求解多分类问题，像线性回归一样。

其优化目标是：

$$\min ~~~\frac{1}{2}Tr((XW-T)^T(XW-T)) \tag{4}$$

其解为：

$$W = (X^TX)^{-1}X^{T}T$$

最小二乘法存在两个缺点：

1. 对噪声敏感
2. 在分类问题上最小二乘法的假设不合理，在很多问题上会失败

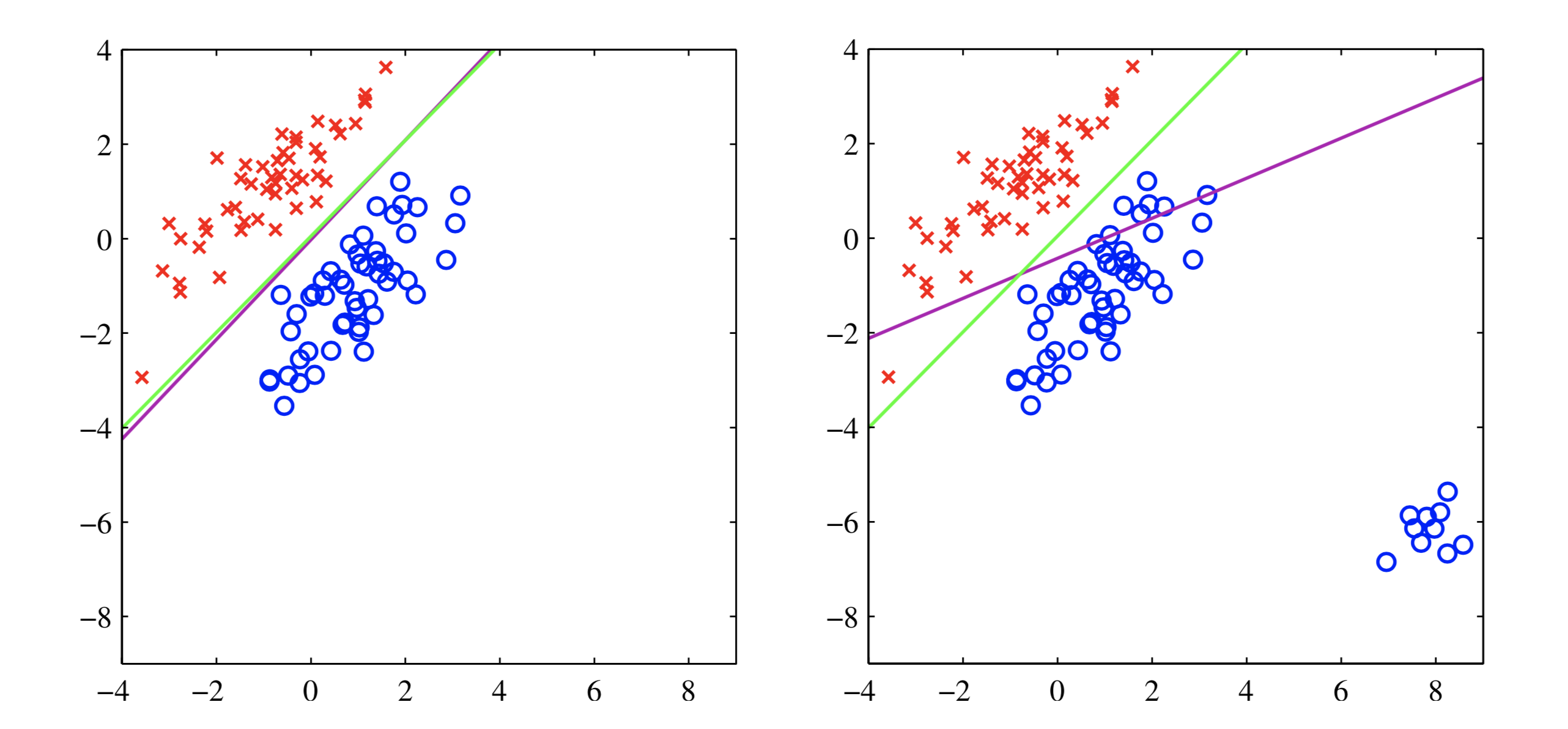
上图反映了最小二乘法对噪声敏感的问题，在右图中，存在一小撮距离较远的点（右下角蓝色），为了使有这一小撮点到分界面的距离（不是垂直距离，是y-y(x)的距离）尽量小（优化目标），分界面会大幅倾斜。

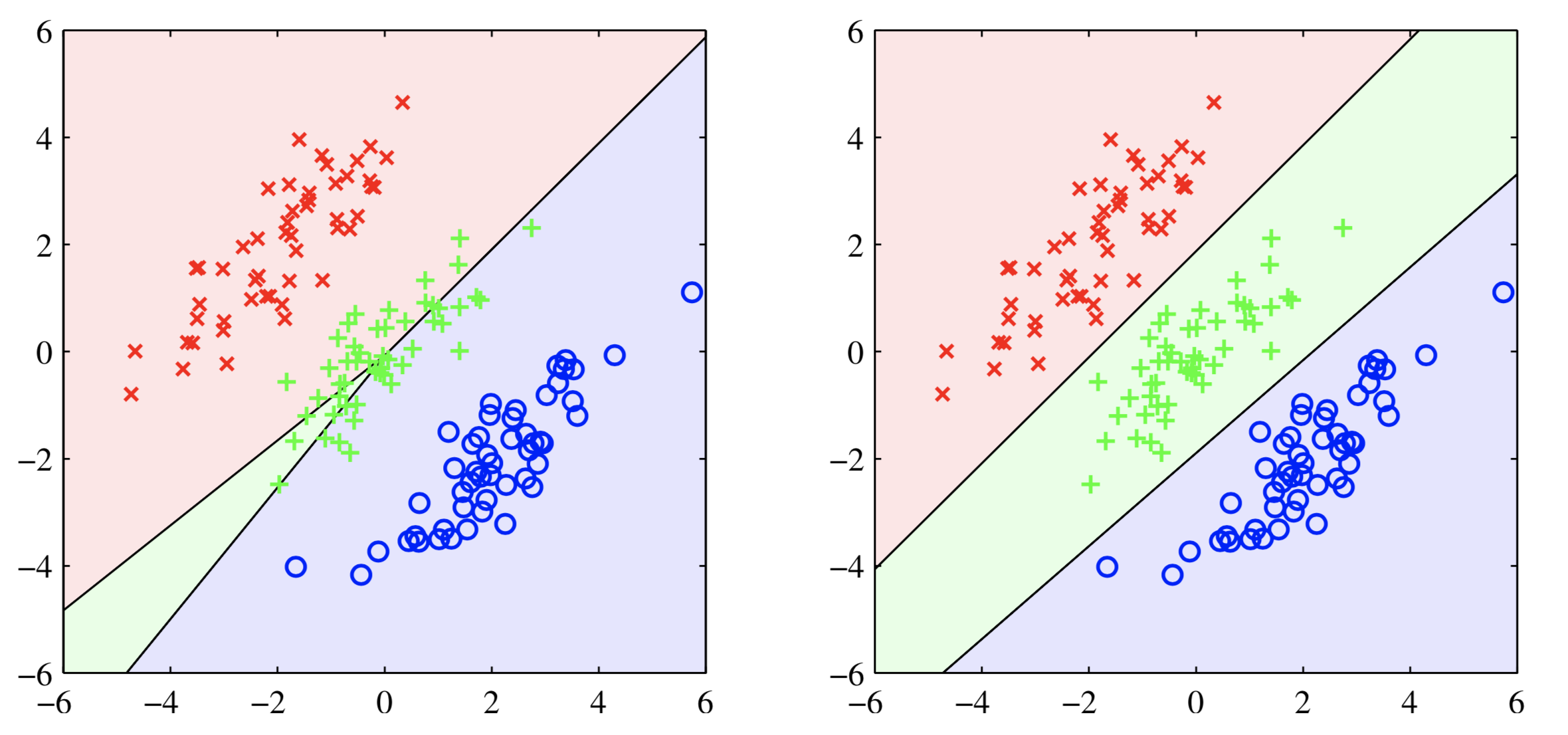
上图反映了最小二乘法分类失败的情景。理想情况下最优的分界面是右图，但是使用最小二乘法只能得到左图的分界面，原因在于最小二乘法基于高斯假设，即假设模型误差服从高斯分布。在这种情况下$p(t|x)$也是服从高斯分布，概率等值线如下：

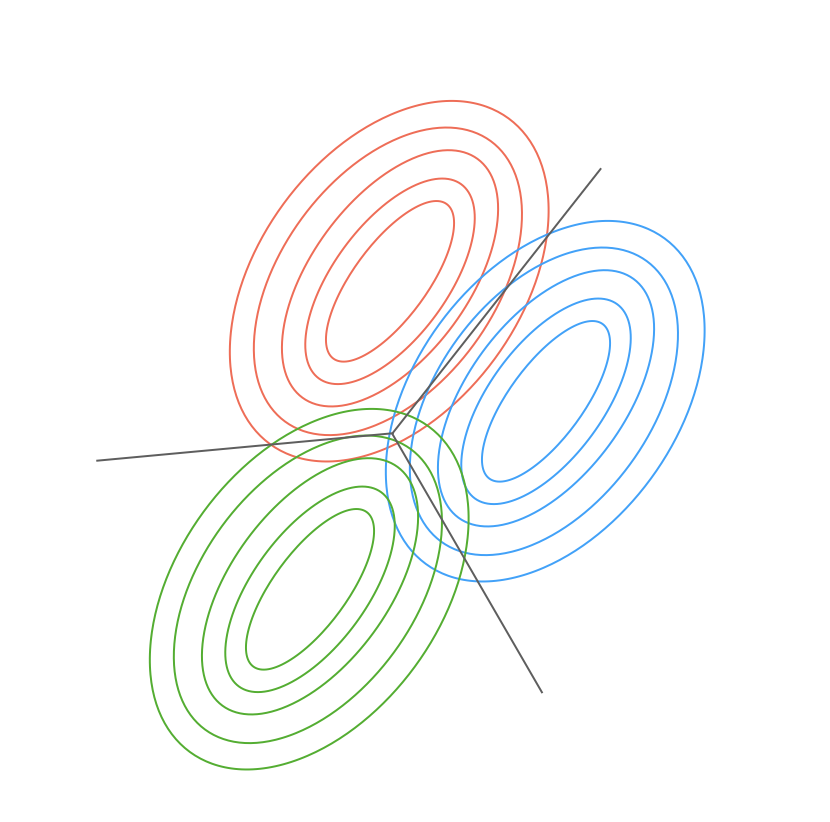
其分界面是$p(t=1|x) = p(t=0|x)$，如上图所示。直观上理解，误差服从高斯分布显然也是不合理的，因为类别标签是0、1，不是连续的。

Fisher’s Linear Discriminant（LDA）

二分类

线性二分类可看成两步：

1. $y(x)=\mathbf{w^{T}x}$将样本$\mathbf{x}$映射到一维
2. 在一维上分类，$y(x)\geq y_0$属于正类，$y(x)<y_0$负类

如果要分类的好，一个朴素的想法就是让样本映射到一维空间后可以分得很开。

假设两类点的中心分别是：

$$\mathbf{m_1} = \frac{1}{N_1}\sum_{n \in C_1} \mathbf{x_n} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathbf{m_2} = \frac{1}{N_2}\sum_{n \in C_2} \mathbf{x_n}$$

则投影之后类别中心是：

$$m_k = \mathbf{w}^{T}\mathbf{m_k}$$

则优化目标为：

$$\max ~~~(m_2-m_1)^2=\mathbf{w^T(m_2-m_1)} ~~~~s.t.~~ \mathbf{w^Tw}=1 \tag{5}$$

使用拉格朗日乘子法：

$$L(\mathbf{w}) =\mathbf{w^T(m_2-m_1)} +\lambda(\mathbf{w^{T}w-1})$$

求得:

$$\mathbf{w} \propto (\mathbf{m_2-m_1})$$

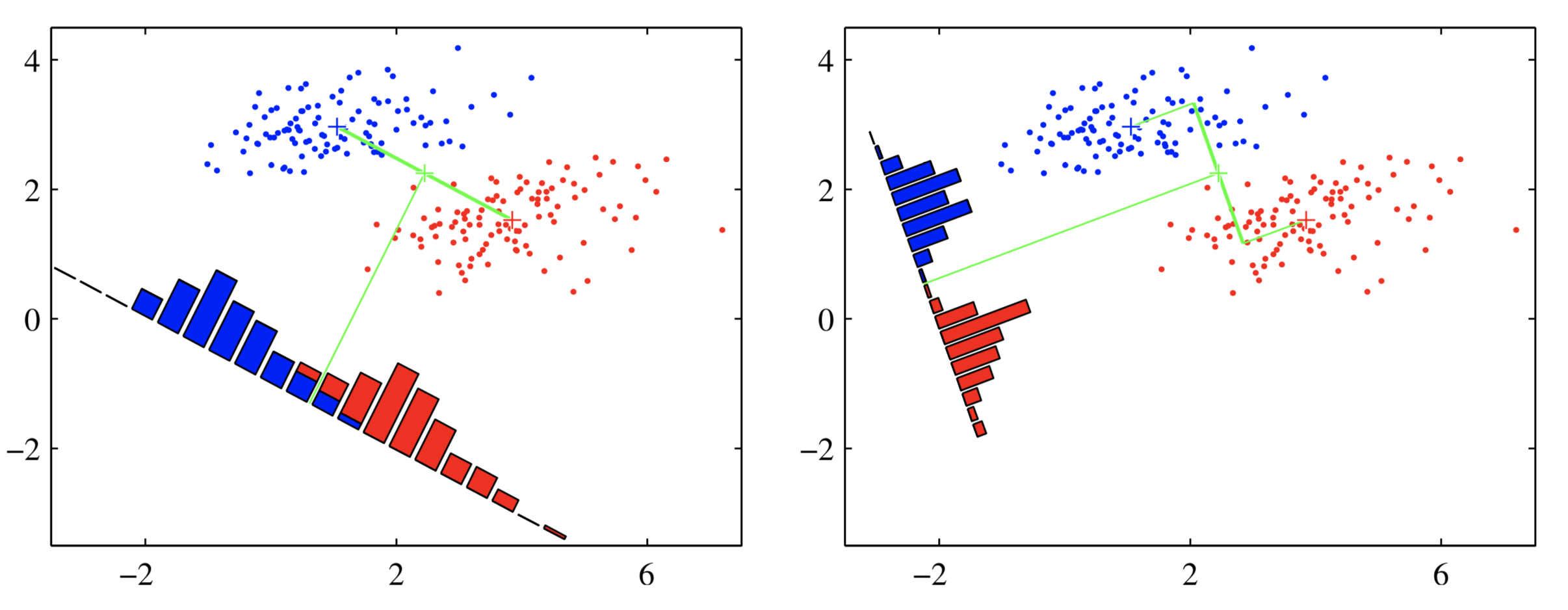
上面左图反映了投影结果，可以看出，仅考虑类中心的距离会导致投影后样本有很多重叠，原因是样本集的协方差不是对角阵。LDA的不仅考虑了类别之间的距离，也考虑了类内的方差。其优化目标是：

$$\max ~~~ J(\mathbf{w}) = \frac{(m_2 - m_1)^2}{s_1^2 + s_2^{2}} = \mathbf{\frac{w^TS_Bw}{w^TS_ww}} \tag{6}$$

其中$s_1, s_2$表示类内方差，定义为：

$$s_k = \sum_{n\in C_k} (y_n - m_k)^2$$

$\mathbf{S_B,S_W}$定义为：

$$\mathbf{S_B = (m_2 -m_1)(m_2-m_1)^T} \\ \mathbf{S_W = \sum_{n \in C_1}(x_n - m_1)(x_n - m_1)^T + \sum_{n \in C_2}(x_n - m_2)(x_n - m_2)^T}$$

式(6)对$\mathbf{w}$求导得到：

$$\mathbf{(w^{T}S_Bw)S_Ww=(w^TS_Ww)S_Bw}$$

即：

$$\mathbf{w \propto S_W^{-1}(m_2-m_1)}$$

当$\mathbf{S_W}$是对角阵并且对角元素都相等的时候(isotropic covariance)，$\mathbf{w \propto (m_2-m_1)}$。

投影之后，可看做一维空间上的分类问题，通过决策理论选择一个阈值后即可构建一个分类器。

多分类

对于K分类问题，类内方差定义为：

$$\begin{aligned} \mathbf{S_W} &= \sum_{k = 1}^{K}\mathbf{S}_k \\ \mathbf{S}_k &= \sum_{n \in C_k}(x_n - \mathbf{m}_k)(x_n - \mathbf{m}_k)^{T} \\ \mathbf{m}_k &= \frac{1}{N_k}\sum_{n \in C_k}\mathbf{x}_n \end{aligned}$$

总方差是：

$$\mathbf{S_T= \sum_{n = 1}^{N}(x_n - m)(x_n-m)^{T}} \\ \mathbf{m} = \frac{1}{N}\sum_{n=1}^{N}\mathbf{x}_n = \frac{1}{N}\sum_{k=1}^{K}N_k\mathbf{m}_k \tag{7}$$

将总方差拆分成两项：

$$\mathbf{S_T =S_W + S_B}$$

将其中$\mathbf{S_B}$当做类间方差：

$$\mathbf{S_B} = \sum_{k =1}^{K}N_k\mathbf{(m_k-m)(m_k-m)^{T}} \tag{8}$$

得到类内方差和类间方差后通过可构建以下优化目标：

$$\max ~~~ J(\mathbf{W}) = \mathbf{Tr \left\{ (W^TS_WW)^{-1}(W^TS_BW)\right\}} \tag{9}$$

该优化目标的解是$\mathbf{S_W^{-1}S_B}$的最大的D个特征值对于的特征向量，D为最后的降维维数。因为(8)由K

个秩为1的矩阵构成，并且因为(7)，自由度仅为K-1，因此$\mathbf{S_B}$的秩最多为K-1，所以$D\leq K-1$。

感知机

感知机采用+1、-1作为类别标签，模型如下：

$$y(\mathbf{x})=f(\mathbf{w^{T}x}) \\ f(a) = \begin{cases} +1 ~~~~~~a \geq 0\\ -1 ~~~~~~a < 0 \end{cases}$$

如果采用分错数量作为损失，最后的损失函数曲线是分段常数函数(piecewise constant)，即每一段都是平的，导数为0，无法优化。感知机采用以下方式作为损失函数，这样最后的损失函数为分段线性(piecewise linear)：

$$E(\mathbf{w}) =-\sum_{n \in M}\mathbf{w}^{T}\mathbf{x}_nt_n$$

对于分错样本$\mathbf{x}_n$，损失$-\mathbf{w}^{T}\mathbf{x}_nt_n > 0$，对于分对样本，损失为0。

使用梯度下降法更新，更新方法如下：

$$\mathbf{w}^{\tau+1} = \mathbf{w}^{\tau} - \eta \bigtriangledown E(\mathbf{w}) =\mathbf{w}^{\tau}+\eta \mathbf{x}_nt_n$$

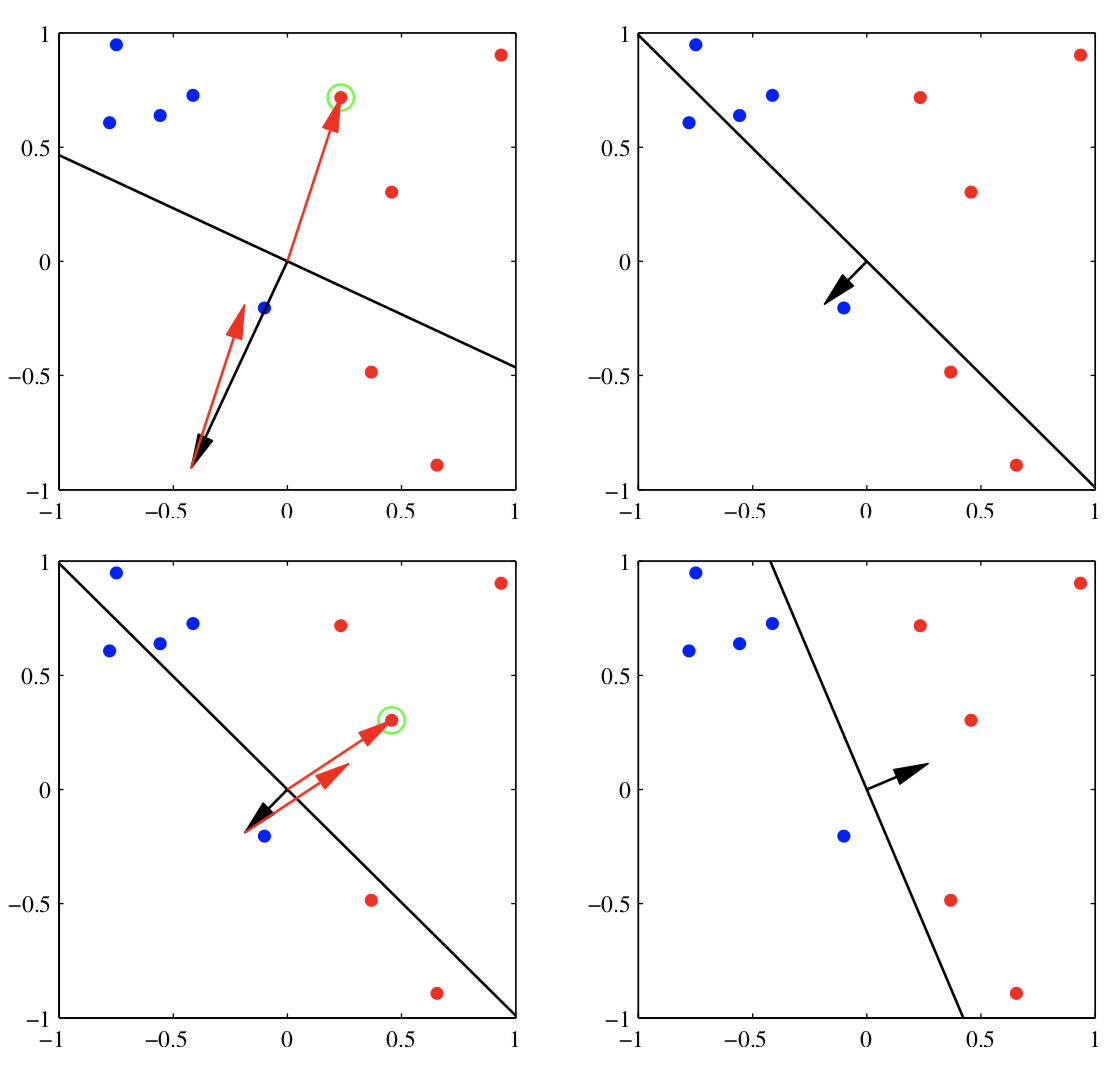
通过上图可以直观理解感知机算法原理。当一个样本$\mathbf{x}_n$分错时，如果是正样本，$\mathbf{w}^{\tau + 1}=\mathbf{w}^{\tau} + \mathbf{x}_n$，如果是负样本，$\mathbf{w}^{\tau + 1}=\mathbf{w}^{\tau} - \mathbf{x}_n$(这里$\eta = 1$)。上图中绿色的圈表示分错了，$\mathbf{w}$加上样本后分界面就会得到纠正。

感知机算法的好处是其收敛性有保证：如果数据能够线性可分，感知机算法能保证收敛。但是，感知机也存在一些缺点。

1. 即使在线性可分的情况下，感知机的收敛性能够得到保证，但是可能会收敛很慢
2. 数据是否线性可分无法判断，感知机的优势其实不明显
3. 不太容易拓展到多分类情况